Unlocking The Secrets Of The Parallelogram Shape: A Comprehensive Guide
The world of geometry is filled with fascinating shapes, each with its own unique characteristics and applications. Among these, the parallelogram shape stands out as a fundamental building block, appearing in everything from architectural designs to everyday objects. Understanding this versatile quadrilateral is not just an academic exercise; it provides a foundational insight into how shapes interact and behave in two-dimensional space. In this article, let us learn about the parallelogram shape, the parallelogram definition, the different types of parallelograms, and how to find the area of a parallelogram. We'll delve into its intriguing properties, explore its special cases, and uncover why this particular geometric form is so prevalent and important. Learn what a parallelogram is, its properties, formulas, and types with examples and diagrams, and learn about its shape, sides, angles, and properties.
A parallelogram is a quadrilateral with two pairs of opposite, parallel sides. It's a shape that only exists in two dimensions, possessing a total of four sides, two pairs of which are parallel to one another. This fundamental definition of a parallelogram is crucial for distinguishing it from other quadrilaterals. We'll also explore how to construct and measure it, ensuring a thorough understanding of this essential geometric figure.
Table of Contents
- What Exactly is a Parallelogram?
- Key Properties of the Parallelogram Shape
- Exploring the Different Types of Parallelograms
- Understanding Angles and Sides in a Parallelogram
- The Role of Diagonals in a Parallelogram
- Symmetry of the Parallelogram Shape
- Calculating the Area of a Parallelogram
- Real-World Applications of the Parallelogram Shape
What Exactly is a Parallelogram?
At its core, a parallelogram is a quadrilateral, meaning it is a polygon with four sides. More specifically, a parallelogram is a quadrilateral in which the opposite sides are parallel and equal. This is the bedrock definition. The definition of a parallelogram is a geometric shape with four sides, and, as the name suggests, two sets of parallel lines. What characterizes a parallelogram is that both parallel pairs are of equal length but don’t need to be equal to the other parallel length. For instance, if you have a four-sided figure where the top and bottom sides are parallel and equal in length, and the left and right sides are also parallel and equal in length, you're looking at a parallelogram.
A parallelogram is a quadrilateral with two pairs of parallel and equal sides and opposite angles. All parallelograms have exactly four corners, four angles, and four sides. A parallelogram is a type of quadrilateral in which the opposite sides are parallel and equal. Each of its four sides has two parallel pairs of sides. Additionally, the lengths of the sides are identical. If the parallel sides are not equal, the shape is not a parallelogram. The form in question is not a parallelogram if the lengths of the parallel sides do not measure the same. This strict adherence to parallel and equal opposite sides is what defines the parallelogram shape and sets it apart from other quadrilaterals.
Key Properties of the Parallelogram Shape
Beyond its fundamental definition, the parallelogram shape boasts several crucial properties that are essential for understanding its behavior and for solving related geometric problems. These properties are not just arbitrary rules; they are direct consequences of the parallel nature of its sides, often stemming from Euclidean geometry principles.
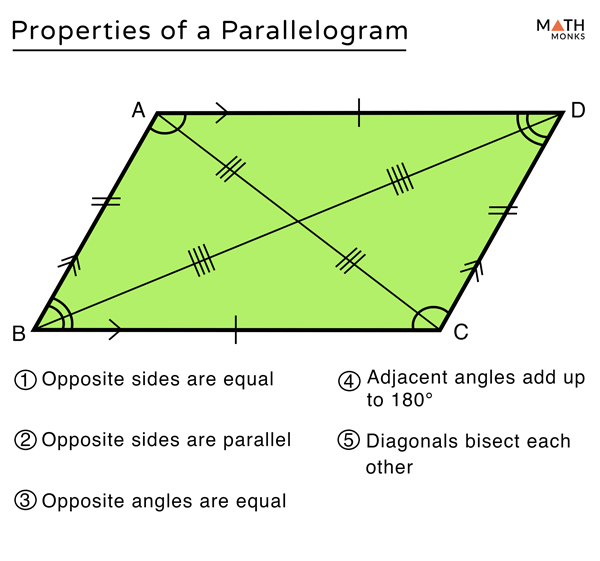
- Opposite Sides are Congruent: The opposite or facing sides of a parallelogram are of equal length. This means if you have a parallelogram ABCD, then side AB will be equal to side CD, and side BC will be equal to side AD. This property is a direct result of the definition.
- Opposite Angles are Congruent: The opposite angles of a parallelogram are of equal measure. For example, angle A will be equal to angle C, and angle B will be equal to angle D. The congruence of opposite sides and opposite angles is a direct consequence of the Euclidean parallel postulate. Similarly to this, a parallelogram must always have equal inner angles on both sides.
- Consecutive Angles are Supplementary: Consecutive angles (angles next to each other) in a parallelogram add up to 180 degrees. This means angle A + angle B = 180°, angle B + angle C = 180°, and so on. This is because consecutive angles are interior angles on the same side of a transversal line cutting through parallel lines.
- Diagonals Bisect Each Other: The diagonals of a parallelogram bisect each other. This means that when the two diagonals intersect, the point of intersection divides each diagonal into two equal segments. We will delve deeper into this property in a dedicated section.
Understanding the properties of parallelograms helps to easily relate its angles and sides. These characteristics are not merely theoretical; they are practical tools for architects, engineers, and anyone working with geometric designs. A parallelogram is a quadrilateral with opposite sides parallel (and therefore opposite angles equal).
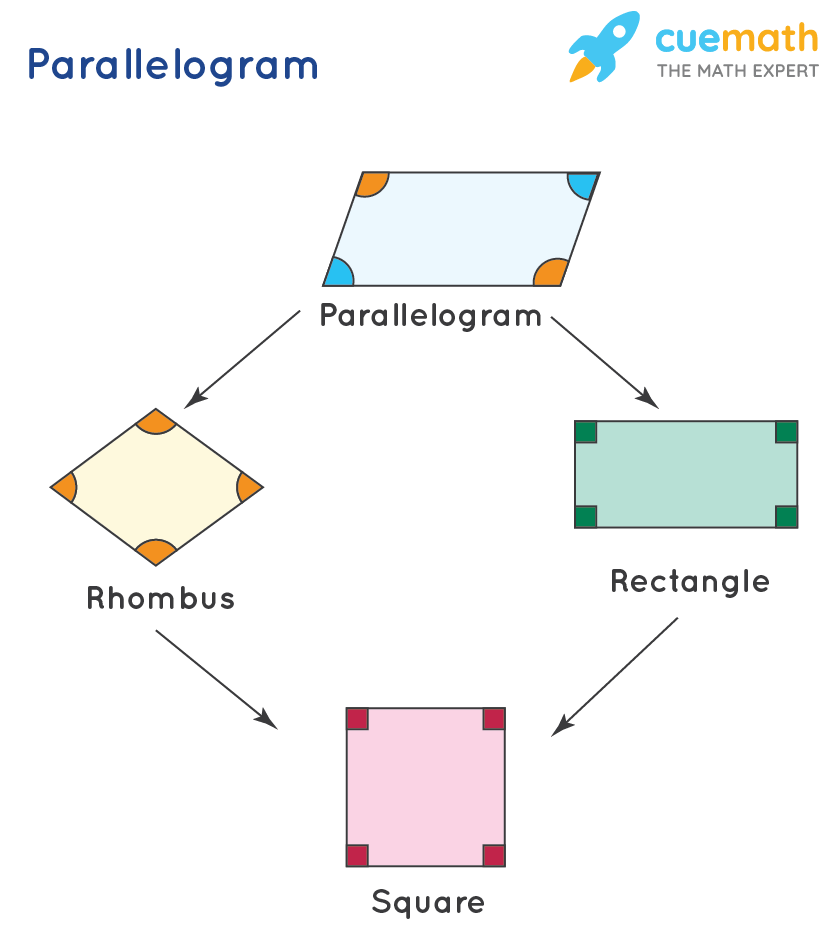
Exploring the Different Types of Parallelograms
While all parallelograms share the core properties mentioned above, some have additional unique characteristics that lead to their classification as special types. Parallelograms are classified into three main types: Square, rectangle, and rhombus, and each of them has its own unique properties. Multiple different shapes are parallelograms. For example, a square, rhombus, and rectangle are also parallelograms. Some types are also included in the definition of other types. Let us look at each type in turn, as they are often sources of confusion.
The Rectangle: A Right-Angled Parallelogram
Is a rectangle a parallelogram? Absolutely! A rectangle is a parallelogram whose angles are all right angles. This means every internal angle of a rectangle measures exactly 90 degrees. Because it is a parallelogram, it inherits all the properties of a general parallelogram: opposite sides are parallel and equal, and its diagonals bisect each other. The added condition of right angles gives it its distinct rectangular appearance, making it a very common and recognizable shape in everyday life, from doors to computer screens.
The Rhombus: A Parallelogram with Equal Sides
A rhombus is another special type of parallelogram. What makes a rhombus unique is that all four of its sides are of equal length. A quadrilateral with equal sides is called a rhombus. Like a rectangle, a rhombus retains all the properties of a general parallelogram: opposite sides are parallel, opposite angles are equal, and diagonals bisect each other. However, in a rhombus, the diagonals also intersect at right angles, and they bisect the angles of the rhombus. This gives the rhombus its characteristic "diamond" shape, which can be seen in various designs and patterns.
The Square: The Ultimate Parallelogram
The square is arguably the most "perfect" of all parallelograms, as it combines the defining features of both a rectangle and a rhombus. A square is a parallelogram that has all four sides equal in length (like a rhombus) AND all four angles are right angles (like a rectangle). And, since a square is a degenerate case of a rectangle, both squares and rectangles are special types of parallelograms. This makes the square a highly symmetrical and versatile shape, used extensively in construction, art, and mathematics. It possesses all the properties of a parallelogram, a rectangle, and a rhombus, making it a truly exceptional quadrilateral.
Understanding Angles and Sides in a Parallelogram
A parallelogram has two dimensions. As we've established, a parallelogram is a quadrilateral in which the opposite sides are parallel (figure \(\pageindex{3}\) if we were to refer to a diagram). This parallelism directly influences the relationships between its angles and sides. The opposite angles of a parallelogram are equal in measure, and the sum of adjacent angles of a parallelogram is equal to 180 degrees. There are four angles in a parallelogram at the vertices.
Let's consider a parallelogram with vertices A, B, C, and D, moving clockwise. Side AB is parallel to side CD, and side BC is parallel to side AD. Furthermore, the length of side AB is equal to the length of side CD, and the length of side BC is equal to the length of side AD. Additionally, the parallel sides have the same length. If the parallel sides are not equal, the shape is not a parallelogram. The lengths of the sides are identical. The form in question is not a parallelogram if the lengths of the parallel sides do not measure the same.
Regarding angles, angle A is equal to angle C, and angle B is equal to angle D. The sum of any two consecutive angles, such as angle A and angle B, will always be 180 degrees. This supplementary relationship is a key characteristic that helps in solving problems involving parallelogram angles. Understanding these precise relationships between sides and angles is fundamental to mastering the parallelogram shape.
The Role of Diagonals in a Parallelogram
The polygon diagonals of a parallelogram are fascinating lines that reveal even more about its internal structure. A diagonal is a line segment that connects two non-adjacent vertices of a polygon. In a parallelogram, there are always two diagonals. To discover its properties, we will draw a diagonal, a line connecting the opposite vertices of the parallelogram. For example, in parallelogram ABCD, AC and BD are the diagonals.
One of the most significant properties related to diagonals is that they bisect each other. This means they cut each other exactly in half at their point of intersection. If the diagonals AC and BD intersect at point E, then AE = EC and BE = ED. This property is unique to parallelograms and is not necessarily true for all quadrilaterals.
Another interesting aspect is that bisecting a parallelogram along a diagonal divides the figure into two congruent triangles. For instance, drawing diagonal AC in parallelogram ABCD creates two triangles, ABC and CDA. These two triangles are congruent, meaning they have the same size and shape. This congruence is a powerful tool in geometric proofs and problem-solving, as it allows us to transfer properties from one triangle to the other within the parallelogram.
Symmetry of the Parallelogram Shape
Symmetry is an important concept in geometry, describing how a shape can be transformed while remaining unchanged. The parallelogram shape exhibits a particular type of symmetry known as rotational symmetry. Specifically, a parallelogram has rotational symmetry of order 2. This means that if you rotate the parallelogram 180 degrees about its center point, it will look exactly the same as its original shape.
Imagine a parallelogram and locate its center, which is the point where its diagonals intersect. Rotating the parallelogram above 180° about point E (the center of rotation) will result in a parallelogram that is the same as the original shape. This is distinct from reflectional symmetry (mirror symmetry), which most parallelograms do not possess unless they are special types like rectangles or rhombuses. A general parallelogram does not have lines of symmetry, but its rotational symmetry is a consistent and defining characteristic. This property is often utilized in design and engineering where shapes need to fit together or repeat in a pattern after a certain rotation.
Calculating the Area of a Parallelogram
One of the most practical applications of understanding the parallelogram shape is being able to calculate its area. The area of a parallelogram is the measure of the two-dimensional space it occupies. Unlike a rectangle, where the area is simply length times width, a parallelogram often has slanted sides, which requires a slightly different approach.
The formula for the area of a parallelogram is the product of the length of its base (b) and height (h). This can be written as: Area = base × height (A = b × h). The base (b) is the length of any one of its sides. The height (h) is the perpendicular distance between that chosen base and its opposite parallel side. It's crucial to remember that the height is not necessarily the length of one of the slanted sides; it's the altitude, which forms a right angle with the base. The height of a parallelogram is the length of an altitude.
For example, if a parallelogram has a base of 10 units and a perpendicular height of 5 units, its area would be 10 × 5 = 50 square units. This formula is derived from the fact that a parallelogram can be transformed into a rectangle of equivalent area by cutting off a right-angled triangle from one end and attaching it to the other. This simple yet powerful formula allows us to quantify the space covered by any parallelogram shape, which is invaluable in fields like construction, land surveying, and graphic design.
Real-World Applications of the Parallelogram Shape
The parallelogram shape is not just a theoretical concept confined to geometry textbooks; it is pervasive in the real world, often without us even realizing it. Its unique properties make it ideal for various practical applications across different industries.
- Architecture and Construction: Many structures utilize the parallelogram shape for stability and aesthetic appeal. Think of slanted roofs, bridge supports, or even the design of modern buildings. The ability of a parallelogram to maintain its shape under stress, especially when reinforced, makes it a strong structural element.
- Engineering and Mechanics: Parallelograms are fundamental in the design of mechanisms. For instance, a common application is in scissor lifts or car jacks, where the parallel sides allow for vertical movement while maintaining a stable base. The pantograph, a mechanical linkage used to copy drawings at different scales, is another excellent example of parallelograms in action.
- Art and Design: Artists and designers frequently incorporate the parallelogram shape to create perspective, depth, and dynamic compositions. From abstract paintings to graphic design layouts, the inherent balance and directionality of parallelograms add visual interest and structure.
- Everyday Objects: Look around your home or office, and you'll find parallelograms everywhere. Books, laptop screens (when viewed at an angle), and even the tiles on your floor might be rectangular, a special type of parallelogram. When you push a rectangular box and it tilts, it temporarily forms a parallelogram.
- Sports and Games: The layout of a baseball diamond, while primarily a square, has elements that can be analyzed using parallelogram properties. Even in games and quizzes, understanding this shape is crucial. Solve practice problems on parallelograms and test your knowledge with games and quizzes to solidify your understanding.
These examples highlight how the principles of the parallelogram shape are applied to solve real-world problems and create functional and beautiful designs. Its versatility stems directly from its defining characteristics.
Conclusion
In this comprehensive guide, we've taken a deep dive into the fascinating world of the parallelogram shape. We've learned that a parallelogram is a fundamental quadrilateral defined by two pairs of parallel and equal opposite sides. We explored its key properties, including the congruence of opposite sides and angles, the supplementary nature of consecutive angles, and the crucial fact that its diagonals bisect each other. Furthermore, we distinguished between the various types of parallelograms—the rectangle, rhombus, and square—understanding how each is a special case inheriting all the core properties while adding its own unique characteristics.
We also touched upon the rotational symmetry of the parallelogram and, importantly, learned how to calculate its area using the simple formula of base times height. From its abstract geometric definition to its myriad applications in architecture, engineering, and everyday objects, the parallelogram shape proves to be a cornerstone of two-dimensional geometry. Mastering the parallelogram shape provides a robust foundation for understanding more complex geometric concepts and for appreciating the mathematical elegance hidden in the world around us.
We hope this article has provided you with a clear and thorough understanding of parallelograms. Do you have any favorite real-world examples of parallelograms? Share your thoughts in the comments below! If you found this article helpful, consider sharing it with others who might benefit from learning about this essential geometric figure, and explore our other articles for more insights into the world of shapes and mathematics.
Parallelogram - Shape | Definition | Formulas, Properties, Examples

Parallelogram | Solved Examples | Geometry - Cuemath
Parallelogram – Definition, Shape, Properties, Formulas